Биткойн: система цифровой пиринговой наличности ₿
Сатоши Накамото,
satoshin@gmx.com
www.bitcoin.org
Переведено на русский по bitcoin.org/bitcoin.pdf
Аннотация.
Полностью одноранговое устройство системы электронных денег
позволяет совершать электронные транзакции между участниками напрямую, минуя любые финансовые институты. Частично, эту задачу решает использование цифровых подписей, но необходимость доверенного лица для контроля за двойной тратой лишает этот подход основных преимуществ. Мы предлагаем децентрализованное решение проблемы двойной траты с использованием одноранговой (пиринговой) сети. Сеть ставит метки времени на транзакции, соединяя их в цепочку доказательств проделанной работы на основе хэширования. Сформированные таким образом записи невозможно
изменить, не выполнив заново всего объема вычислений. Самая длинная версия цепочки служит не только подтверждением очередности событий, но и доказывает, что над ней произвел работу самый большой вычислительный
сегмент сети. До тех пор пока большая часть вычислительных мощностей контролируется узлами, не объединенными с целью атаковать сеть, они будут генерировать самую длинную цепочку, опережая любых злоумышленников.
Устройство самой сети очень простое: сообщения рассылаются на основе принципа «наименьших затрат», а узлы могут покидать сеть и снова подключаться к ней в любой момент, принимая самую длинную версию цепочки для восстановления пропущенной истории транзакций.
1 Введение
Интернет-коммерция в большинстве случаев опирается на финансовые учреждения, выступающие в роли доверенных посредников для проведения электронных платежей. Такая схема хорошо работает для большинства транзакций, но в ее основе лежит доверие, что влечет определенные проблемы. Необходимое посредничество финансовых институтов препятствует осуществлению необратимых транзакций. Цена этих услуг увеличивает стоимость транзакций и устанавливает минимальную их цену, делая непрактичным проведение нечастых и небольших транзакций. Кроме того, отсутствие необратимых транзакций увеличивает и стоимость сервисов, чьи услуги являются неотменяемыми. Поскольку платеж можно аннулировать, продавец вынужден быть настороже, требуя от покупателя больше информации, чем в принципе необходимо. И определенный процент мошенничества принимается просто как неизбежность. Эти наценки и неопределенности с платежами могут быть преодолены в случае делок с бумажной наличностью, однако механизма для проведения прямых электронных транзакций не существует. Необходима платежная система, основанная на криптографии, а не на доверии, которая позволила бы любым двум участникам осуществить перевод средств напрямую, без участия посредника. Вычислительная дороговизна отмены транзакций оградила бы продавцов от мошенничества, а легкоосуществимые механизмы эскроу защитили бы покупателей. В данной работе мы предлагаем решение проблемы двойной траты, основанное на распределенном одноранговом сервере меток времени, который своей вычислительной мощностью подтверждает хронологический порядок транзакций. Система находится в безопасности, пока под совокупным контролем ее честных участников находится больше вычислительной мощности, чем под контролем группы действующих совместно злоумышленников.
2 Транзакции
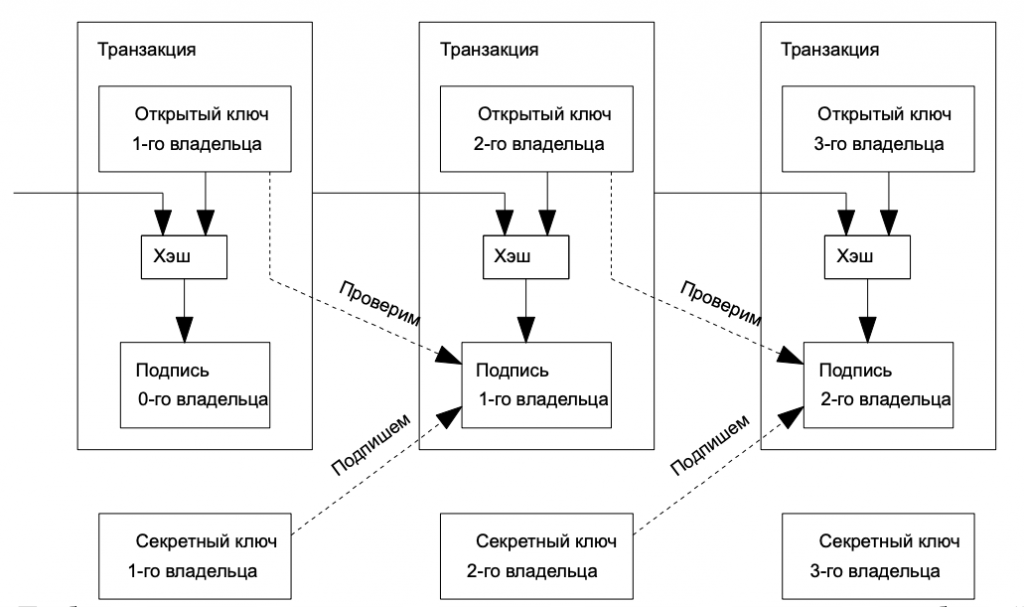
Определим электронную монету как последовательность цифровых подписей. Очередной владелец отправляет монету следующему, подписывая хэш предыдущей транзакции и публичный ключ будущего владельца и присоединяя эту информацию к монете. Получатель может проверить каждую подпись, чтобы подтвердить корректность всей цепочки владельцев.
Проблема, разумеется, в том, что получатель не может определить, сколько раз бывший владелец потратил эту монету. Традиционное решение заключается в проверке центральным доверенным лицом («монетным двором» или эмитентом) каждой транзакции.
После любого платежа монета возвращается к эмитенту, который выпускает новую ее версию; и только напрямую полученным таким образом монетам можно доверять.
Недостаток этого подхода в том, что от компании-эмитента зависит судьба всей денежной системы, так как она подобно банку контролирует каждую проходящую через нее транзакцию.
Адресат должен знать, что никто из предыдущих владельцев не подписал транзакцию, предшествующую по времени той, что находится в цепочке отправленной ему монеты. Для наших целей лишь первая транзакция из нескольких является истинной, поэтому мы не должны беспокоиться о поздних попытках двойной траты. В централизованной модели эмитент знал обо всех транзакциях и решал, в каком порядке они идут. Чтобы избавить схему от посредника, участникам необходимо открыто публиковать транзакции [1], а также уметь приходить к согласию относительно единого порядка их следования. Получателю нужно доказательство того, что для каждой транзакции из цепочки большинство пользователей согласны считать ее первой.
3 Сервер меток времени
Начнем описание нашего решения с сервера меток времени. Его работа заключается в хэшировании блока данных, на который нужно поставить метку, и открытой публикации этого хэша, как в газете или Usenet-постах [2-5]. Метка времени показывает, что в данный момент конкретные данные существовали и потому попали в хэш блока. Каждый хэш включает в себя предыдущую метку: так выстраивается цепь, где очередное звено укрепляет все предыдущие.
4 Доказательство работы
Чтобы реализовать распределенный одноранговый сервер меток времени, мы используем схему «доказательства работы», подобную системе Hashcash Адама Бека [6]. Суть заключается в поиске такого значения, чей хэш (например, SHA-256) начинался бы с некоторого числа нулевых битов. Требуется выполнить объем работы, экспоненциально зависящий от числа нулей, но для проверки найденного значения достаточно вычислить лишь один хэш.
В нашем сервере меток времени поиск значения с нужным хэшем происходит путем перебора значения итерируемого поля-добавки (nonce) в блоке данных. Как только блок, удовлетворяющий условию, найден, его содержимое нельзя изменить, не выполнив заново всей работы. И если он не является последним в цепочке, эта работа включает в себя и перевычисление всех блоков, следующих за ним.
Доказательство работы через хэширование также решает вопрос об определении версии, поддерживаемой большинством. Если голосом считается один IP-адрес, то такую схему можно скомпроментировать, если контролировать большой диапазон адресов. Наша схема основана на принципе «один процессор — один голос». Самая длинная из хэш-цепочек выражает мнение большинства, которое вложило в нее наибольшее количество ресурсов. Если более половины вычислительной мощи принадлежит честным узлам, то цепочка честных транзакций будет расти быстрее и опередит любую конкурирующую цепь. Чтобы внести изменения в любой из прошлых блоков, атакующему придется выполнить заново работу над этим блоком и всеми последующими, а затем догнать и перегнать честных участников по новым блокам. Ниже мы покажем, что вероятность такого успеха у злоумышленника, обладающего меньшими ресурсами, экспоненциально убывает в зависимости от числа блоков.
Для компенсации возрастающей вычислительной мощи процессоров и колебания числа работающих узлов в сети, сложность хэширования должна изменяться, чтобы обеспечивать равномерную скорость генерации блоков. Если они появляются слишком часто — сложность возрастает, и наоборот.
5 Сеть
Система работает по следующим правилам:
- Новые транзакции рассылаются всем узлам.
- Каждый узел объединяет пришедшие транзакции в блок.
- Каждый узел пытается подобрать хэш блока, удовлетворяющий текущей сложности.
- Как только такой хэш найден, этот блок отправляется в сеть.
- Узлы принимают блок, только если все транзакции в нем корректны и не используют уже потраченные средства.
- Свое согласие с новыми данными узлы выражают, начиная работу над следующим блоком и используя хэш предыдущего в качестве новых исходных данных.
Участники всегда считают истинной самую длинную версию цепочки и работают над ее удлинением. Если два узла одновременно опубликуют разные версии очередного блока, то кто-то из остальных пиров получит раньше одну версию, а кто-то — другую. В таком случае каждый начнет работать над своей версией цепочки, сохранив другую на случай, если она окажется продолжена раньше. Двойственность исчезнет, как только будет получен новый блок, который продолжит любую из ветвей, и те узлы, что работали над конкурирующей версией, переключатся на нее.
Новые транзакции не обязательно должны достигать всех узлов. Если о них будет знать достаточно много узлов, вскоре они попадут в один из блоков. Правила рассылки блоков тоже не являются строгими в отношении потерянных сообщений. Как только узел, пропустивший один из блоков, получит уже следующий за ним, он запросит недостающую информацию, чтобы заполнить очевидный пропуск.
6 Стимулы
По умолчанию, первая транзакция в блоке является специальной, создающей новую монету, которая принадлежит создателю блока. Такая схема поощряет честных участников сети, стимулируя их поддерживать работу сети, а также решает вопрос о начальном распределении денежной массы в отсутствие центрального эмитента. Равномерное увеличение числа монет в обращении можно сравнить с добычей золота, в которую золотоискатели тоже вкладывают свои ресурсы. В роли последних в нашем случае выступают процессорное время и электричество.
Другим способом стимулирования может быть комиссия за транзакции. Если входная сумма платежа больше выходной, то разница является комиссией за перевод и прибавляется к базовому значению награды за найденный блок в первой транзакции. Как только суммарный объем денежной массы достигнет заранее установленного максимума, единственным источником поощрения работы над блоками останутся комиссии, при этом избавленные от инфляции.
Такая форма стимулирования может также способствовать уменьшению случаев мошенничества. Если жадный злоумышленник способен выделить больше вычислительных мощностей, чем все честные участники, он может обманывать продавцов, аннулируя свои транзакции и возвращая средства, или же направить свои ресурсы на генерацию новых блоков и монет. Более выгодным для него является вариант «игры по правилам», который обеспечивает получение более половины всех новых денег, чем вариант «саботажа системы» и поддержания своего капитала на постоянном уровне.
7 Экономия дискового пространства
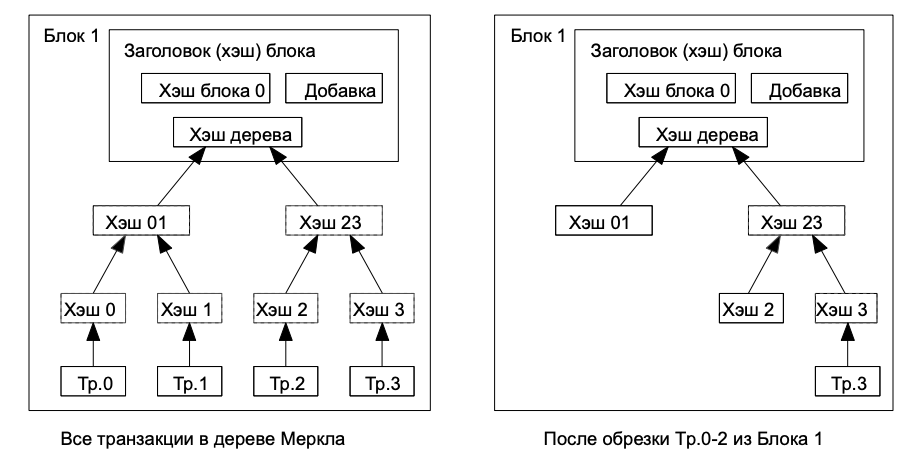
Как только последняя транзакция в монете-цепочке окажется внутри достаточно старого блока, все предшествующие ей транзакции в цепочке могут быть удалены в целях очистки дискового пространства. Чтобы хэш блока остался неизменным, все транзакции в блоке хранятся в виде хэш-дерева Меркла [7][2][5] и лишь его корень включается в хэш блока. Размер старых блоков может быть уменьшен за счет удаления ненужных ветвей этого дерева, хранить промежуточные хэши необязательно.
Заголовок пустого блока будет составлять около 80 байт. Из расчета скорости генерации блока раз в десять минут получаем 80624*365=4.2 Мб в год. Для среднестатистического на 2008 год компьютера с 2 Гб оперативной памяти с учетом закона Мура, предсказывающего рост на 1.2 Гб в год, хранение данных не будет проблемой, даже если все заголовки блоков будут находиться в памяти.
8 Упрощенная проверка платежей
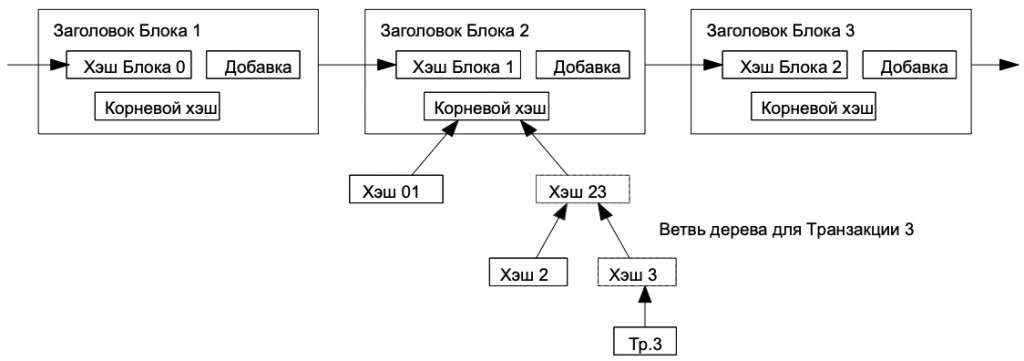
Верификация транзакций возможна без запуска полнофункционального узла. Пользователю необходимо лишь хранить заголовки блоков самой длинной цепочки, которую он получил от других узлов, и запрашивать хэш-поддерево для необходимой транзакции. Он не может проверить корректность транзакции самостоятельно, но получив ссылку на блок, в котором она находится, он может убедиться в том, что этот блок и все последующие приняты и подтверждены сетью.
Самая длинная цепочка доказательств работы:
На такой метод проверки можно полагаться, пока сеть хотя бы наполовину находится под контролем честных участников, то есть пока злоумышленник не завладеет большими ресурсами. Обычные узлы могут проверять транзакции самостоятельно, но если нападающий генерирует самую длинную цепь блоков, то своими сфабрикованными транзакциями он может скомпроментировать упрощенную схему. Одной из стратегий противодействия этому может быть рассылка сигналов тревоги от обычных пиров, которые
получают «ложный» блок. Такой сигнал будет заставлять программу-клиент загружать блок полностью, чтобы самостоятельно подтверждать некорректность данных. Компании, часто принимающие платежи, возможно, будут подключаться к сети в обычном режиме для большей независимости, безопасности и быстроты проверки.
9 Соединение и разделение сумм
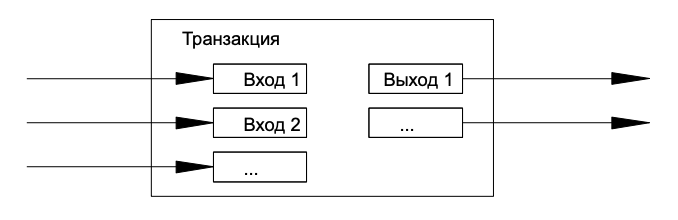
Несмотря на то, что можно оперировать отдельными монетами, создавать специальную транзакцию для каждого цента было бы слишком неудобно. Для поддержки разделямых и объединяемых сумм транзакции содержат несколько входов и выходов. Обычная транзакция будет выглядеть так: либо один вход от предыдущего крупного платежа, либо несколько входов, аккумулирующих небольшие суммы, и не более двух выходов: один является собственно платежом, а другой, если необходимо, возвращает «сдачу» обратно отправителю.
Необходимо отметить, что увеличение связей, когда транзакция зависит от нескольких, а те в свою очередь зависят от еще большего числа, не является проблемой, поскольку нет необходимости получать полную и независимую копию истории транзакции.
10 Конфиденциальность
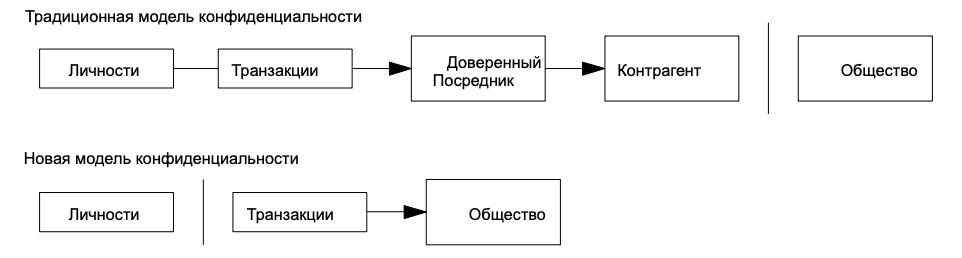
Традиционная банковская модель поддерживает необходимый уровень конфиденциальности, предоставляя доступ к информации лишь сторонам-участницам и доверенному третьему лицу. Необходимость открытой публикации транзакций исключает такой подход, однако приватность по-прежнему можно сохранить, если публичные ключи будут анонимными. Открытой будет информация о том, что кто-то отправил кому-то некоторую сумму, но без привязки к конкретным личностям. Столько же данных раскрывается и на фондовых биржах, которые публикуют время и объем частных сделок, не указывая, между кем именно они были совершены.
Дополнительной защитой будет являться генерация новой пары «открытый/закрытый ключ» для каждой транзакции: это предотвратит связывание различных платежей с их общим отправителем или адресатом. Некоторого публичного связывания все же не избежать: транзакции с несколькими входами доказывают, что эти суммы принадлежат одному лицу. Риск состоит в том, что раскрытие личности владельца ключа может привести к раскрытию и всех принадлежащих ему транзакций.
11 Оценка
Рассмотрим сценарий, в котором злоумышленник пытается генерировать более длинную цепь блоков, чем честные участники. Даже если он преуспеет, это не приведет к тому, что можно будет создавать деньги из воздуха, присваивать себе чужие монеты или вносить иные произвольные изменения. Узлы никогда не примут некорректную транзакцию или блок, ее содержащий. Атакующий может лишь пытаться изменить одну из своих транзакций, чтобы возвратить себе деньги.
Гонку между честными участниками и нападающим можно представить как биномиальное случайное блуждание. Успешное событие, когда «хорошая» цепь удлиняется на один блок, приводит к увеличению отрыва на единицу, а неуспешное, когда очередной
блок создает злоумышленник, — к его сокращению. Вероятность атакующего наверстать разницу в несколько блоков такая же, как и в задаче о «разорении игрока». Представим, что игрок имеет неограниченный кредит, начинает с некоторым дефицитом и у него есть бесконечно много попыток, чтобы отыграться.
Вероятность того, что он преуспеет, как и вероятность злоумышленника догнать честых участников, вычисляется следующим образом [8]:
p = вероятность появления блока в честной цепочке
q = вероятность того, что блок создаст атакующий
qz = вероятность того, что атакующий наверстает разницу в z блоков
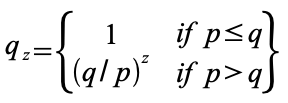
В случае p > q вероятность уменьшается экспоненциально с ростом числа блоков, на которое отстает злоумышленник. Поскольку все ставки против него, без удачного рывка в начале его шансы на успех становятся ничтожно малы.
Рассмотрим теперь, как долго получателю платежа стоит ждать, прежде чем он будет полностью уверен, что бывший владелец не сможет отменить транзакцию. Мы предполагаем, что злоумышленник-отправитель позволяет адресату некоторое время верить, что платеж был проведен, после чего возвращает деньги себе. Получатель узнает об этом, но мошенник надеется, что будет уже слишком поздно.
Адресат создает новую пару ключей и сообщает свой публичный ключ отправителю прямо перед подписанием транзакции. Это не позволит отправителю заранее начать работать над цепочкой и провести транзакцию в тот момент, когда он будет достаточно удачлив, чтобы совершить рывок вперед. После отправки платежа мошенник начинает втайне работать над параллельной версией цепочки, содержащей альтернативную транзакцию
Получатель ждет, пока транзакция не будет добавлена в блок и пока тот не будет продолжен еще z блоками. Ему неизвестен прогресс злоумышленника, но если средняя скорость генерации честных блоков — известная величина, то число блоков нападающего подчиняется распределению Пуассона с математическим ожиданием:
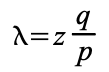
Чтобы получить вероятность того, что атакующий обгонит честных участников, мы умножаем значение случайной величины (число созданных им блоков) на вероятность того, что он сможет наверстать оставшуюся разницу:
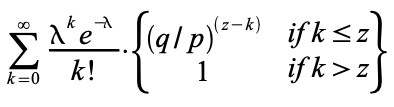
Перегруппировав слагаемые и избавясь от бесконечного ряда, получаем:
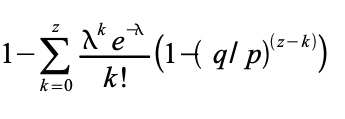
Код программы на языке Си выглядит так:
#include <math.h>
double AttackerSuccessProbability(double q, int z)
{
double p = 1.0 - q;
double lambda = z * (q / p);
double sum = 1.0;
int i, k;
for (k = 0; k <= z; k++)
{
double poisson = exp(-lambda);
for (i = 1; i <= k; i++)
poisson *= lambda / i;
sum -= poisson * (1 - pow(q / p, z - k));
}
return sum;
}Запустив программу, мы видим, что вероятность экспоненциально падает с ростом z:
q=0.1
z=0 P=1.0000000
z=1 P=0.2045873
z=2 P=0.0509779
z=3 P=0.0131722
z=4 P=0.0034552
z=5 P=0.0009137
z=6 P=0.0002428
z=7 P=0.0000647
z=8 P=0.0000173
z=9 P=0.0000046
z=10 P=0.0000012
q=0.3
z=0 P=1.0000000
z=5 P=0.1773523
z=10 P=0.0416605
z=15 P=0.0101008
z=20 P=0.0024804
z=25 P=0.0006132
z=30 P=0.0001522
z=35 P=0.0000379
z=40 P=0.0000095
z=45 P=0.0000024
z=50 P=0.0000006Решая относительно P < 0.1%, получаем:
P < 0.001
q=0.10 z=5
q=0.15 z=8
q=0.20 z=11
q=0.25 z=15
q=0.30 z=24
q=0.35 z=41
q=0.40 z=89
q=0.45 z=34012 Заключени
В данной работе нами была предложена система электронных транзакций, не основанная на доверии. Построение схемы началось с традиционного представления монет на основе цифровых подписей, обеспечивающего контроль владения, но допускающего двойную трату. Эту проблему мы решили посредством пиринговой сети и схемы «доказательства работы» для записи публичной истории транзакций. Попытка злоумышленника, не обладающего большей частью ресурсов сети, изменить старые записи, вычислительно становится практически неосуществимой. Сильной стороной сети является простота ее структуры. Все узлы работают самостоятельно, иногда обмениваясь информацией. Нет необходимости в индентификации, поскольку сообщения не идут по какому-то определенному маршруту, а основе принципа «наименьших затрат». Узлы могут покидать сеть и вновь подключаться, принимая самую длинную цепочку блоков как подтверждение пропущенной истории транзакций. Они выражают свое согласие принять корректный блок в цепочку, используя свои вычислительные мощности для удлинения этой цепи, или несогласие (если блок содержит неверные данные), не продолжая эту цепочку. Любые необходимые правила протокола могут быть реализованы через данный механизм голосования.
Список Литературы:
- W. Dai, «b-money,» http://www.weidai.com/bmoney.txt, 1998.
- H. Massias, X.S. Avila, and J.-J. Quisquater, «Design of a secure timestamping service with minimal trust requirements,» In 20th Symposium on Information Theory in the Benelux, May 1999.
- S. Haber, W.S. Stornetta, «How to time-stamp a digital document,» In Journal of Cryptology, vol 3, no 2, pages 99-111, 1991.
- D. Bayer, S. Haber, W.S. Stornetta, «Improving the efficiency and reliability of digital time-stamping,» In Sequences II: Methods in Communication, Security and Computer Science, pages 329-334, 1993.
- S. Haber, W.S. Stornetta, «Secure names for bit-strings,» In Proceedings of the 4th ACM Conference on Computer and Communications Security, pages 28-35, April 1997.
- A. Back, «Hashcash — a denial of service counter-measure,» http://www.hashcash.org/papers/hashcash.pdf, 2002.
- R.C. Merkle, «Protocols for public key cryptosystems,» In Proc. 1980 Symposium on Security and Privacy, IEEE Computer Society, pages 122-133, April 1980.
- W. Feller, «An introduction to probability theory and its applications,» 957.